一笔画游戏:探索数学的趣味与智慧

数学,作为一门严谨的学科,往往给人留下枯燥无味的印象。在数学的世界里,隐藏着许多充满趣味和智慧的奥秘。一笔画游戏便是其中之一,它不仅能够激发我们对数学的兴趣,还能锻炼我们的逻辑思维和空间想象力。
一、一笔画游戏的起源与发展

一笔画游戏起源于18世纪,由瑞士数学家欧拉提出。最初,它只是一个数学问题,但随着时间的推移,一笔画游戏逐渐演变成一种流行的数学游戏。如今,它已经成为许多数学竞赛和科普活动的重要组成部分。
二、一笔画游戏的基本规则

一笔画游戏的基本规则非常简单:在平面上,由多条线段构成的图形能否一笔画成,使得每条线段只画一次且不重复?例如,汉字“日”和“中”都可以一笔画成,而“田”和“目”则不能。
三、一笔画游戏的解题技巧
要解决一笔画问题,我们需要了解以下几个关键概念:
奇点与偶点:从一点出发的线的数目是单数条,那么这个点就是奇点;如果从一点出发的线的数目是双数条,那么这个点就是偶点。
连通图:一个图形各部分总是有边相连的。
欧拉定理:能一笔画的图形必须是连通图。具体来说,凡是由偶点组成的连通图,一定可以一笔画成;凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
四、一笔画游戏的应用
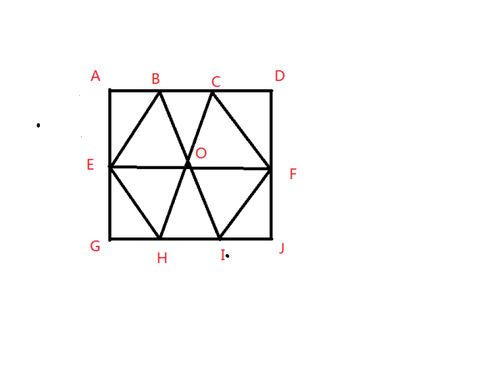
一笔画游戏在现实生活中有着广泛的应用。例如,在地图设计、电路设计、网络布局等领域,都需要考虑如何将图形一笔画成,以节省空间和提高效率。
五、一笔画游戏的趣味性
六、一笔画游戏的挑战与启示
一笔画游戏虽然简单,但要想真正掌握其中的奥秘,并非易事。在挑战过程中,我们可能会遇到各种困难,但正是这些困难,让我们更加珍惜每一次的突破和进步。一笔画游戏启示我们,在追求知识的过程中,要有耐心、有毅力,勇于面对挑战,不断超越自我。
一笔画游戏是数学世界中的一颗璀璨明珠,它既具有趣味性,又具有实用性。通过探索一笔画游戏的奥秘,我们可以更好地理解数学的魅力,培养自己的逻辑思维和空间想象力。让我们在数学的海洋中畅游,尽情享受一笔画游戏带来的乐趣吧!